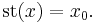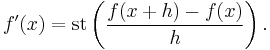Standard part function

In non-standard analysis, the standard part function is a function from the limited (finite) hyperreals to the reals, which associates to every hyperreal, the unique real infinitely close to it. As such, it is a mathematical implementation of the historical concept of adequality introduced by Pierre de Fermat.^[1] The standard part function was first defined by Abraham Robinson as a key ingredient in defining the concepts of the calculus, such as the derivative and the integral, in non-standard analysis. The latter theory is a rigorous formalisation of calculations with infinitesimals.

1 Definition
2 Not internal
3 Applications
4 Notes
5 See also
6 References

Definition

Nonstandard analysis deals primarily with the hyperreal line. The latter is an extension of the real line which contains, in addition to the reals, also infinitely small quantities. In the hyperreal line every real number has a collection of numbers (called a monad) of hyperreals infinitely close to it. The standard part function associates to a finite hyperreal x, the unique standard real number x₀ which infinitely close to it. The relationship is expressed symbolically by writing

$\,\mathrm{st}(x)=x_0.$

The standard part of any infinitesimal is 0. Thus if N is an infinite hypernatural, then 1/N is infinitesimal, and st(1/N) = 0.

Not internal

The standard part function "st" is not defined by an internal set. There are several ways of explaining this. Perhaps the simplest is that its domain L, which is the collection of limited (i.e. finite) hyperreals, is not an internal set. Namely, since L is bounded (by any infinite hypernatural, for instance), L would have to have a least upper bound if L were internal, but L doesn't have a least upper bound. Alternatively, the range of "st" is 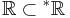$\mathbb{R}\subset {}^*\mathbb{R}$ which is not internal; in fact every internal subset of $\mathbb{R}$ is necessarily finite, see (Goldblatt, 1998).

Applications

The standard part function is used to define the derivative of a function f. If f is a real function, and h is infinitesimal, and if f′(x) exists, then

$f'(x) = \operatorname{st}\left(\frac {f(x%2Bh)-f(x)}h\right).$

Notes

^ Karin Usadi Katz and Mikhail G. Katz (2011) A Burgessian Critique of Nominalistic Tendencies in Contemporary Mathematics and its Historiography. Foundations of Science. DOI: 10.1007/s10699-011-9223-1 [1] See arxiv. The authors refer to the Fermat-Robinson standard part.

References

H. Jerome Keisler: Elementary Calculus: An Infinitesimal Approach. First edition 1976; 2nd edition 1986. (This book is now out of print. The publisher has reverted the copyright to the author, who has made available the 2nd edition in .pdf format available for downloading at http://www.math.wisc.edu/~keisler/calc.html.)

Goldblatt, Robert: Lectures on the hyperreals. An introduction to nonstandard analysis. Graduate Texts in Mathematics, 188. Springer-Verlag, New York, 1998.

Infinitesimals

History	Adequality Infinitesimal calculus Leibniz's notation Integral sign Criticism of non-standard analysis The Analyst The Method of Mechanical Theorems Cavalieri's principle

Related branches of mathematics	Non-standard analysis Non-standard calculus Internal set theory Synthetic differential geometry Constructive non-standard analysis

Formalizations of infinitesimal quantities	Differentials Hyperreal numbers Dual numbers Surreal numbers

Individual concepts	Standard part function Transfer principle Hyperinteger Increment theorem Monad Internal set Levi-Civita field Hyperfinite set Law of Continuity Overspill Microcontinuity

Scientists	Gottfried Leibniz Abraham Robinson Pierre de Fermat Augustin-Louis Cauchy

Infinitesimals in physics and engineering	Infinitesimal strain theory Infinitesimal oscillations of a pendulum

Textbooks	Analyse des Infiniment Petits Elementary Calculus